Decimal a Octal | Recursivo | Prolog | SWI-PROLOG

El sistema octal es un sistema de numeración posicional de base 8. Los símbolos que se usan en este sistema son:

0, 1, 2, 3, 4, 5, 6, 7

Para indicar que un número está escrito en base 8, usamos el subíndice ${}_{(8}$, y para indicar que un número está escrito en base 10, usamos el subíndice ${}_{(10}$.

Ejemplos:

• ${13}_{(8}={11}_{(10}$
• ${25}_{(8}={21}_{(10}$
• ${1077}_{(8}={575}_{(10}$
• $7_{(8}=7_{(10}$

Ejemplo, para la conversión de 49 a octal se realizan los siguientes pasos.

1.- Se divide X entre 8 y se mantiene el residuo para su impresión.

2.- Si el producto de este es menor a 8 se deja de dividir . 

3.- Si el producto es mayor a 8 se vuelve a dividir hasta que el producto sea menor

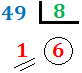
El resultado es el siguiente el residuo de 49/8 es 1 y su producto es 6, como su producto es menor a 8 termina de dividirse y el resultado se lee de derecha a izquierda = 61(8

Bien, teniendo la base de lo que es un numero en sistema octal vamos a sacar nuestras reglas en prolog:

1.- El numero a convertir debe ser un numero mayor a 8.

2.- Si el numero a convertir es menor a 8 se asigna su valor así mismo, es decir si el valor a convertir es 6 entonces el resultado es 6.

3.- El residuo de la división debe mantenerse par armar el resultado.

Código. 

decOct(A,B):-A<8, B is A,write(B).

decOct(A,B):-A>8,C is A//8,X is A mod 8,write(X),decOct(C,B).

Ejecución:

decOct(49,B).
16
B = 6 ;
false.

decOct(768,B).
0041
B = 1 ;
false.

decOct(6,B).
6

B = 6